Key terms constantly pop up in videos and tutorials, but the meaning of each term can be a little fuzzy. So, let’s break them all the way down. But not in a boring way. In a cool, fun way where the definitions are straightforward and the diagrams are colorful.
In this post we’ll explore how sound is produced, the difference between noise and music, and the most essential components of a musical sound; frequency, amplitude and timbre.
Noise vs. Music
Sound is produced when something strikes a physical object and it starts to vibrate in the surrounding medium, which is air. This vibration creates a change in the air pressure which causes the air molecules to move around and try to become stable again. As the vibration travels through the air, it funnels into our ears and reaches our brains as a sound.
An instrument or musical sound creates a change in the air pressure which is known as oscillation. A waveform is a way of visualizing this change in air pressure.
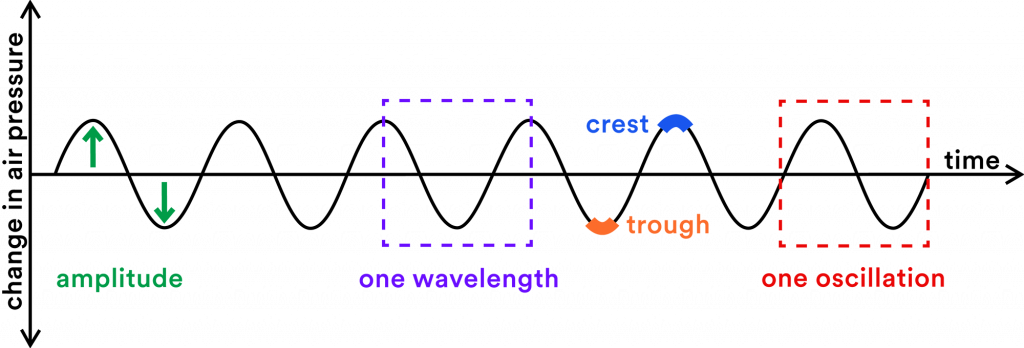
A musical sound creates a waveform that is periodic, meaning that it is orderly, patterned and recurs at fixed intervals. The green waveform below clearly has a pattern.

While noise creates a chaotic and irregular waveform. There is no identifiable repeating pattern in the blue waveform below.

Musical instruments are designed to produce soundwaves that are regular, ordered, and patterned because orderly sounds are aesthetically appealing and we can’t get enough of them. Whereas the sound of your neighbor’s dog barking or cars honking can be grating and unwelcome disturbances.
Next up, I’ll break down three main parameters of musical sound; frequency, amplitude and timbre.
Frequency
Frequency refers to how frequently a sound wave oscillates per second.
A sound wave that oscillates very quickly will produce a higher pitch while a sound wave that oscillates very slowly will produce a lower pitch.


Frequency is measured in Hertz (Hz) which indicates the number of times the sound wave oscillates each second. The prefix “kilo-“ means thousand. So 3,000 herts is the same as 3 kilohertz (kHz).
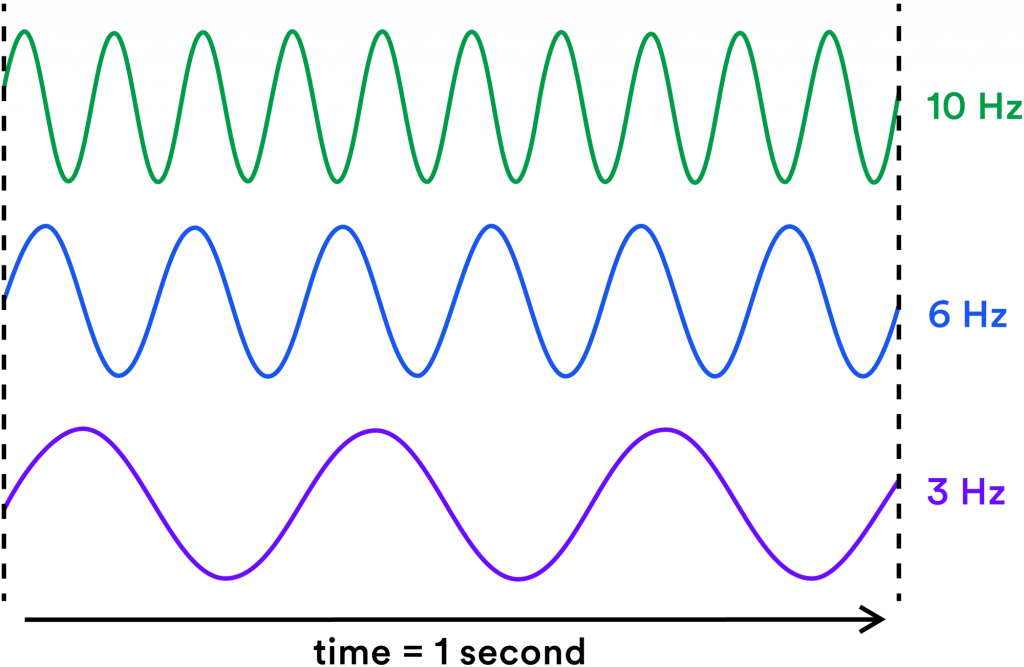
Our hearing range is about 20 Hz – 20 kHz and we lose the ability to hear the higher frequencies as we get older.
The range of frequencies used in music generally spans the range of a concert grand piano, which is about seven octaves.

Amplitude
Amplitude is commonly known as loudness or volume. However, amplitude is a more specific term. Loudness is subjective, while amplitude directly relates to how much the air pressure changes when a musical sound is produced.
When looking at a waveform, the horizontal line (x-axis) acts as a baseline; representing stable air pressure or silence. Where the waveform rises above the line, that indicates an increase in air pressure. Where the waveform drops below the line, that indicates a drop in air pressure.
The distance that the wave rises and drops shows the amplitude or loudness. A quiet sound will stay relatively close to the horizontal line while a loud sound will ascend and descend farther away from the horizontal line.

Amplitude is measured in decibels (dB).
Charles Dodge and Thomas Jerse describe decibels as a “logarithmic unit of relative measurement used to compare the ratio of the intensities of two signals.”
So, a level of volume measured in dB expresses the ratio of a value (eg: the change of air pressure in a room) to a reference value (0 db; the quietest level of sound that the human ear can pick up).
Because decibels are measured logarithmically, 100 dB does not actually have twice the amplitude of 50 dB.
Here is a comparison of a linear and logarithmic scale. In the linear scale the numbers increase by an additive factor. In the logarithmic scale the numbers increase by a multiplicative factor.

As you can see, the logarithmic scale is useful when you’re working with a very large dynamic range. Another reason why we use a logarithmic unit of measurement is that, as humans, we perceive the intensity of sensations like light and sound logarithmically rather than linearly.
Another element of amplitude that is particularly relevant to musicians working with computers is velocity. Within a MIDI track, velocity refers to the variation of volume intensity of each beat or note. This variation is what gives something like a drum pattern or a plucked string pattern created in MIDI a much more realistic sensation by mimicking the variety of intensity a musician would use to play the physical instrument.
Timbre
Sounds in the physical world and the sounds that you create with a synthesizer are complex. A complex tone means that the sound contains a unique blend of frequencies, known as partials. Partials create the distinct timbre (pronounced TAM-ber) or tone quality of an instrument. This quality makes it easy for our ears to distinguish between different sounds and instruments. Understanding timbre also makes it possible to reverse engineer and recreate practically any musical sound.
Complex tones create nonsinusoidal waveforms.

A nonsinusoidal waveform has a more complex pattern than a sine wave because it shows the sum of each of the partials contained in the complex tone. Looking at a nonsinusoidal waveform is like looking at a particular shade of paint. By looking at the paint you can see that it is a shade of magenta, but you do not know what exact mixture of colors was used to create that shade. So, you either need a magical method to unmix the paint or to learn the mixture formula.
When you unmix a complex waveform, you’ll find that it is entirely composed of sine waves.
A sine wave or sinusoid is a perfectly periodic wave that is composed of a single frequency. Thus, a sine wave is a pure tone.

Nothing in the physical world can produce a pure tone sine wave other than a computer or synthesizer. However, you can recreate practically any musical sound using sine waves.
The layered frequencies that create a distinct timbre are known as the harmonic spectrum, harmonics, partials, and overtones. These terms are often used interchangeably which makes it difficult to keep them straight. I’m going to do my best to untangle these terms in this section.
So, let’s break down a complex tone.
This is a sawtooth wave. For the sake of this example, let’s say we created this sawtooth wave by playing middle C on a wavetable synthesizer:
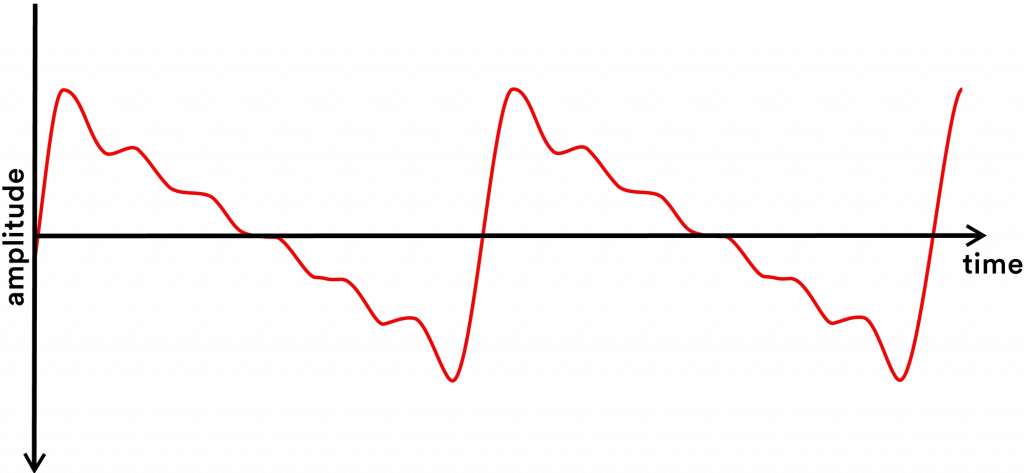
So, the pitch for this example is middle C (256 Hz). The pitch is determined by the fundamental frequency. The fundamental frequency is the lowest frequency partial and the loudest partial.
Here is that sawtooth wave with the fundamental frequency overlaid on top of it in red:
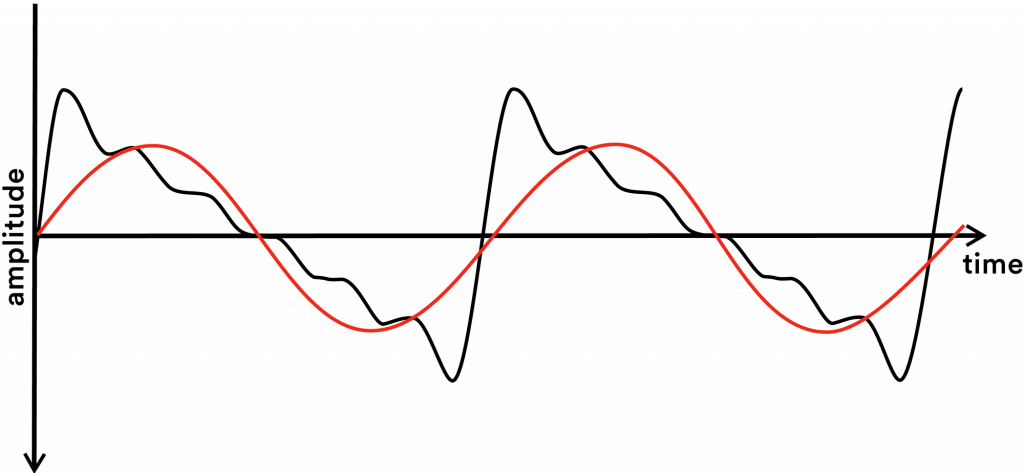
The partials that create distinct tone quality are the harmonics and inharmonics. The harmonic series is an ideal set of frequencies in which each harmonic is a positive integer (a whole number greater than zero) multiple of the fundamental frequency. It is ideal because it is based on mathematical theories that do not manifest themselves perfectly in the real world.
Therefore, most pitched instruments still produce some faint inharmonic partials. An inharmonic partial is a partial that does not match an ideal harmonic. Some instruments, such as bells, timpani, marimba and vibraphone, contain mostly inharmonic partials.
Back to our sawtooth wave; This is what the first 5 harmonics of our sawtooth wave look like:

In the table below you can see that the harmonic spectrum is composed of a series of harmonics. Each harmonic is a positive integer multiple (a whole number greater than zero) of the fundamental frequency (f). The first harmonic is the fundamental frequency (f) multiplied by 1, therefore it is in unison with the fundamental as it is sounding the exact same frequency.

To recap: All the frequencies in a complex sound are partials. The lowest partial is called the fundamental frequency which determines the pitch.
All harmonics are partials but not all partials are harmonics — only the ones that match up with the harmonic spectrum. Those that do not match up are inharmonic partials.
Any partial that is above the fundamental frequency can also be called an overtone. The term overtone is used often, but it has no special meaning other than to refer to all the partials excluding the fundamental frequency.
In theory, the harmonic spectrum could continue ad infinitum. But, since our time here is finite, I’m only demonstrating the first 5 harmonics.
Fourier Analysis
I made an analogy to unmixing a shade of paint earlier. I don’t know if it’s possible to unmix paint but we actually can unmix complex tones.
The process of analyzing and decomposing a complex musical sound is called Fourier Analysis. The Fourier series was discovered by the French mathematician Jean-Baptiste Joseph Fourier (1768-1830) which is used to perform Fourier Analysis. This method shows how any complex periodic sound can be analyzed as the sum of many different sine waves of varying frequencies.
Sine waves are extremely interesting for this reason. Any musical sound can be decomposed into a series of sine waves and then recreated using those sine waves. I never took trigonometry or calculus in school so I won’t endeavor to understand the mathematical side too deeply. However, it is extremely cool just to have a basic conceptual understanding of this principal if you are interested in synthesis. If your curiosity is piqued, you can learn more about Fourier Analysis with this video here.
If there are any concepts or terminology you’d like me to cover in future Sound & Synthesis installments, please send me an email or post a comment below ?






